Review AI504 Practice Session

0. NumPy

행렬이나 일반적으로 대규모 다차원 배열을 쉽게 처리 할 수 있도록 지원하는 파이썬의 라이브러리이다. (출처: 위키피디아)

How to use? import numpy as np

1. NumPy array data

Scalar : single number
- e.g. a = np.array(1.)
Vectors : an array of numbers
- e.g. b = np.array([1., 2., 3.])
Matrix : 2-D array
- e.g. c = np.array([[1., 2., 3.], [4., 5., 6.]])
Tensor : N-dimensional array (n ≥ 2)
- e.g. d = np.array([[[1., 2., 3.], [4., 5., 6.]], [[7., 8., 9.], [10., 11., 12.]]])

https://hadrienj.github.io/posts/Deep-Learning-Book-Series-2.1-Scalars-Vectors-Matrices-and-Tensors/

Functions

.ndim : show dimension

e.g.

a.ndim → 0

b.ndim → 1

c.ndim → 2

d.ndim → 3
.shape : show the number of values for each dimension

e.g.

a.shape → ()

b.shape →(3,)

c.shape → (2,3)

d.shape → (2, 2, 3)

💡 NOTE : → 뒤는 **출력값(Output)**을 의미

2. Define Numpy arrays

np.ones(shape) : define array given shape and fill with 1

e.g. (10,) shape를 가지면서 1으로 채워진 배열을 정의

usage : np.ones(10)
np.zeros(shape) : define array given shape and fill with 0

e.g. (2,5) shape를 가지면서 0으로 채워진 배열을 정의

usage : np.zeros((2,5))
np.full(shape, number) : define array given shape and fill with given number

e.g. (2,5) shape를 가지면서 5로 채워진 배열을 정의

usage : np.full((2,5),5)
np.random.random(shape) : define array given shape and fill with random numbers

e.g. (2,3,4) shape를 가지는 랜덤 배열 정의

usage : np.random.random((2, 3, 4))
np.arange(number) : define array which contains 0 to given number-1 (similar to python range())

e.g. 0~9로 구성된 배열

usage : np.arrange(10)

→ array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
- np.arange(number).astype(type) : define arange() array given data type
  
  e.g. float 타입의 0~9로 구성된 배열
  
  usage : np.arange(10).astype(float)
  
  → array([0., 1., 2., 3., 4., 5., 6., 7., 8., 9.])
- np.arrange(number).reshape(shape) : define arange() array given shape
  
  e.g.(5, 2) shape를 가지면서 0~9로 구성된 배열
  
  usage : np.arange(10).reshape((5,2))
  
  → array([[0, 1], [2, 3], [4, 5], [6, 7], [8, 9]])

💡 NOTE : shape를 명시할 때, shape가 2-by-3 이면, 괄호까지 포함해서 **(2,3)**로 명시하기!
e.g. 🙅🏻‍♀️ np.ones(2,3) 🙆🏻‍♀️ np.ones((2,3))

3. Indexing & Slicing

python에서의 indexing & slicing 과 동일하게 작동한다.

e.g. a = np.arange(10) b = np.arange(9).reshape(3,3)

a[index] : access index of a, and index could be < 0

e.g. a의 0번째 인덱스에 있는 값

usage : a[0] → 0

e.g. a의 뒤에서 4번째에 있는 값

usage : a[-4] → 6

e.g. 마지막 row

usage : b[-1] → [6 7 8]
- Conditional indexing : 조건문에 따른 인덱싱 가능
  
  e.g. 짝수인 값만 출력
```
idx = b % 2 == 0
# -> [[True False  True]
#     [False  True False]
#     [True False  True]]
b[idx]
# -> [0 2 4 6 8]
```
- Specific elements from a nd-array
  
  e.g. [0, 2, 3] index에 대한 값 출력 (vector)
```
idx = [0, 2, 3]
a[idx]
# [0 2 3]
```
  e.g. [0, 2] 행 혹은 열에 해당하는 값 출력 (tensor)
```
idx = [0, 2]
# row
b[idx, :]
# -> [[0 1 2]
#     [6 7 8]]

# column
b[:,idx]
# -> [[0 2]
#     [3 5]
#     [6 8]]
```
  e.g. [[0,0,1],[1,2,0]]에 해당하는 값 출력 (tuple 형태도 가능)
```
idx = np.array([[0,0,1],[1,2,0]])
# tuple : idx = ((0,0,1),(1,2,0))
b[idx]
# -> [[[0 1 2]
#      [0 1 2]
#      [3 4 5]]
#     [[3 4 5]
#      [6 7 8]
#      [0 1 2]]]
```
a[start index:end index:interval] : access from start index to end index - 1 with interval, and interval could be < 0

e.g. 2번째부터 4번째 인덱스에 있는 값

usage : a[2:5] → [2 3 4]

e.g. 0번째부터 10번째 인덱스 이전까지 있는 값을 3을 간격으로 출력

usage : a[0:10:3] → [0 3 6 9]

e.g. 8번째부터 5번째 인덱스 다음까지 있는 값을 -1을 간격으로 출력

usage : a[8:5:-1] → [8 7 6]

e.g. 두번째 column

usage : b[:,1] → [1 4 7]

4. Math Operations

Element-wise operation

+, - , x, / : given two numpy arrays should have same shape

e.g.

a = np.arange(6).reshape((3, 2))
b = np.full((3,2),2)

print(a+b)
# -> [[2 3]
#     [4 5]
#     [6 7]]

print(a-b)
# -> [[-2 -1]
#     [ 0  1]
#     [ 2  3]]

print(a*b)
# -> [[ 0  2]
#     [ 4  6]
#     [ 8 10]]

print(a/b)
# -> [[0.  0.5]
#     [1.  1.5]
#     [2.  2.5]]

Unary operation

e.g. a = np.arange(6).reshape((3,2))
- a.sum(axis) : get sum of a regarding axis (axis is optional)
  
  usage : a.sum() → 15
  
  e.g. axis 0에 대한 sum (row-wise)
  
  usage : a.sum(axis=0) → [6 9]
  
  e.g. axis 1에 대한 sum (column-wise)
  
  usage : a.sum(axis=1) → [1 5 9]
- a.mean() : get mean of a → 2.5
- a.max() : get maximum value of a → 5
- a.min() : get minimum value of a → 0
Dot product, Multiplication

e.g.

vector : a = np.arange(3).astype('float') b = np.ones(3)

matrix : a = np.arange(6).reshape((3, 2)) b = np.arange(6).reshape((2, 3))

tensor : a = np.arange(24).reshape((4, 3, 2)) b = np.ones((4, 2, 3))
- Dot product
  
  usage : np.dot(a, b)
  - vector : np.dot(a, b) → 3.0
  - matrix : np.dot(a, b).shape → (3, 3)
  - tensor : np.dot(a, b).shape → (4, 3, 4, 3)
- Mutiplication
  
  usage : a@b
  - vector : a@b → 3.0
  - matrix : (a@b).shape → (3, 3)
  - tensor : (a@b).shape → (4, 3, 3)

5. Shape Manipulation

Reshape

usage : a.reshape(shape)

shape 에서 -1 은 주어진 수가 있을 경우, 현재 shape에서 주어진 수만큼의 모양을 가지고 남는 차원으로 할당하고, 주어진 수가 없을 경우, 1차원 배열로 만든다. 그리고 -1을 통해 가능한 차원 추가는 한 차원 추가만 가능하다.

e.g.

a = np.arange(24)
b = a.reshape((6, 4))
print(b.shape)
c = a.reshape((6, -1))
print(c.shape)
# b와 c의 shape는 (6,4)로 동일
d = a.reshape((6,4,-1))
print(d.shape)
# d의 shape는 (6, 4, 1)이 됨
# d = a.reshape((6,4,-1,-1)) -> ValueError: can only specify one unknown dimension
e = b.reshape(-1)
# e의 shape는 a에서의 shape와 동일하게 (24,)가 됨

Add an extra dimension

usage : a[:, None]

차원 추가하기 원하는 부분에 None을 입력하고, 기존 값들은 [:] slicing을 통해 복사

e.g.

a = np.arange(3)
print(a.shape) # -> (3,)
b = a[:, None]
print(b)
# -> [[0]
#     [1]
#     [2]]
print(b.shape) # -> (3, 1)
c = a[None, :]
print(c) # -> [0 1 2]
print(c.shape) # -> (1, 3)
d = a[:, None, None]
print(d.shape) # -> (3, 1, 1)

Stack, concatenation

vstack : stack vertically

usage : np.vstack(tuple)
hstack : stack horizontally

usage : np.vstack(tuple)
concatenate : concatenate on axis (default axis = 0)

usage : np.concatenate(tuple, axis)
- axis = 0 이면 vstack의 결과와 동일하고, axis = 1 이면 hstack의 결과와 동일
- axis = None 이면 1차원으로 만들어버림
- axis 에 해당하는 dimension을 제외하고 무조건 나머지 input dimension은 동일해야 함!

e.g.

a = np.ones((3,2))
b = np.zeros((3,2))

print(np.vstack([a, b]))
# -> [[1. 1.]
#     [1. 1.]
#     [1. 1.]
#     [0. 0.]
#     [0. 0.]
#     [0. 0.]]
print(np.hstack([a, b]))
# -> [[1. 1. 0. 0.]
#     [1. 1. 0. 0.]
#     [1. 1. 0. 0.]]
print(np.hstack([a, b, a]))
# -> [[1. 1. 0. 0. 1. 1.]
#     [1. 1. 0. 0. 1. 1.]
#     [1. 1. 0. 0. 1. 1.]]
print(np.concatenate([a, b], axis=0))
# -> [[1. 1.]
#     [1. 1.]
#     [1. 1.]
#     [0. 0.]
#     [0. 0.]
#     [0. 0.]]
print(np.concatenate([a, b], axis=1))
# -> [[1. 1. 0. 0.]
#     [1. 1. 0. 0.]
#     [1. 1. 0. 0.]]

a = np.ones((4,3,2))
b = np.zeros((5,4,2))
np.concatenate([a,b], axis=2) # -> ValueError

a = np.ones((4,3,2))
b = np.zeros((4,3,7))
np.concatenate([a,b], axis=2).shape # -> (4,3,9)

Transpose

Matrix transpose

usage : a.T

e.g.

a = np.arange(6).reshape((3, 2))
b = a.T
print(b.shape) # -> (2, 3)

Tensor transpose

usage : np.transpose(a, axes)

axes : 전체 axis 갯수의 tuple or list of ints 로, 원하는 순서의 axis 들의 나열

e.g.

a = np.arange(24).reshape((4, 3, 2))
b = np.transpose(a, [0, 2, 1])
print(b.shape) # -> (4, 2, 3)
c = np.transpose(a, [1, 0, 2])
print(c.shape) # -> (3, 4, 2)

6. Broadcasting

Broadcasting : 두 배열이 다른 shape를 가지더라도 두 배열의 shape가 조건을 만족한다면, 둘 중 더 작은 dimension이 더 큰 dimension을 가지도록 만들어서 사칙연산이 가능하도록 하는 것을 말한다.

조건 : 동일한 dimension이거나 1이어야 한다.

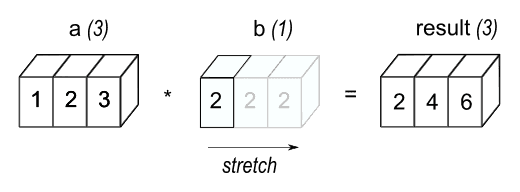https://numpy.org/doc/stable/user/basics.broadcasting.html

e.g.

# Vector and scalar
a = np.arange(3)
b = 2.
print(a+b) # -> [2. 3. 4.]
print(a-b) # -> [-2. -1.  0.]
print(a*b) # -> [0. 2. 4.]
print(a/b) # -> [0.  0.5 1. ]

# Matrix and vector
a = np.arange(6).reshape((3, 2))
b = np.arange(2).reshape((1, 2))
print((a+b).shape) # -> (3, 2)

# Tensor and matrix
a = np.arange(12).reshape((2,3,2))
b = np.arange(6).reshape((3,2))
print((a+b).shape) # -> (2, 3, 2)
print(a + b[None,:]) # -> (2, 3, 2)

Quiz : Fill the function `foo()`

import numpy as np

def sigmoid(x):
    return 1./(1. + np.exp(-x))

def foo(M, W):
	# Define a function that, given M of shape (m,n) and W of shape (4n, n), executes the following:
	# - Take the first half rows of M
	# - Take the second half rows of M
	# - Take the odd-numbered rows of M
	# - Take the even-numbered rows of M
	# - Append them horizontally in the listed order so that you obtain a matrix X of shape (?, 4n)
	# - Linearly transform X with W so that you obtain a matrix Y of shape (?, ?)
	# - Put Y through the sigmoid function
	# - Obtain the sum of the row-wise mean
	
W = np.arange(16).reshape(8,2).astype('float') / 10.
M = (np.arange(20).reshape((10,2)).astype('float') - 10.) / 10.

foo(M, W)

Answer

   import numpy as np
   
   def sigmoid(x):
       return 1./(1. + np.exp(-x))
   
   def foo(M, W):
     (row, col) = M.shape
     first_half_rows = M[:row//2]
     second_half_rows = M[row//2:]
     odd_num_rows = M[1::2]
     even_num_rows = M[0::2]
     X = np.hstack([first_half_rows, second_half_rows, odd_num_rows, even_num_rows])
     # X = np.concatenate([first_half_rows, second_half_rows, odd_num_rows, even_num_rows], axis=1)
     Y = np.dot(X, W)
     sigmoid_Y = sigmoid(Y)
     row_wise_mean = sigmoid_Y.mean(axis=0)
     return np.sum(row_wise_mean)
   
   W = np.arange(16).reshape(8,2).astype('float') / 10.
   M = (np.arange(20).reshape((10,2)).astype('float') - 10.) / 10.
   
   foo(M, W)

0. NumPy
1. NumPy array data
- Functions
2. Define Numpy arrays
3. Indexing & Slicing
4. Math Operations
5. Shape Manipulation
6. Broadcasting
Quiz : Fill the function foo()

0. NumPy

1. NumPy array data

Functions

2. Define Numpy arrays

3. Indexing & Slicing

4. Math Operations

5. Shape Manipulation

6. Broadcasting

Quiz : Fill the function foo()

Quiz : Fill the function `foo()`