Review AI504 Practice Session

1. Matplotlib

NumPy 라이브러리를 활용하여 그래프를 만들어 시각화할 수 있는 라이브러리이다.

지난번 NumPy에 대한 기본적인 설명은 여기에! 👇🏼

https://sunkyoung.github.io/pytorch-study-01/

How to use ?

import matplotlib.pyplot as plt
import numpy as np

Basic usage
- plt.plot(x-axis, y-axis) : 주어진 x축, y축 데이터를 바탕으로 선형 그래프를 그림
- plt.scatter(x-axis, y-axis, s=None, c=None) : 주어진 x축, y축 데이터를 바탕으로 점을 그림
  - s : 점의 크기
  - c : 색깔 지정 (리스트 형태로도 지정가능하며 리스트 길이만큼 cmap과 norm을 mapping하여 색을 표현)
  - e.g. plt.scatter(X, y, s=30, c="red")
- plt.show() : 플롯을 보여줌
- np.linspace(start, end, number_of_sample) : sampling을 위해 주로 사용되는 함수이며, start~end 구간 내에 있는 데이터들을 지정한 개수(number_of_sample) 만큼 균등하게 샘플링하여 array형태로 반환해줌
  - end_point=False 로 설정한다면, 리스트의 인덱싱과 같이 start ~ (end-1) 구간으로 설정되며, 기본 값은 end_point=True
  - e.g.
```
np.linspace(2.0, 3.0, num=5)
# -> array([2.  , 2.25, 2.5 , 2.75, 3.  ])
np.linspace(2.0, 3.0, num=5, endpoint=False)
# -> array([2. ,  2.2,  2.4,  2.6,  2.8])
```

위의 기본 사용법을 바탕으로 그래프를 그려보자!

foo = lambda x: -(2/7*x**3-9/2*x**2+15*x-10.)

X = np.linspace(0, 10, 100)
y = foo(X)

x_sample = np.linspace(0, 10, 5)
y_sample = foo(x_sample)

plt.plot(X, y)
plt.scatter(x_sample, y_sample, c="red", s=30)
plt.xlabel('x')
plt.ylabel('y')
plt.axhline(0, color='black')
plt.axvline(0, color='black')
plt.show()

→ 출력되는 그래프

plot

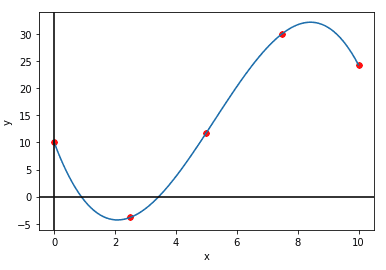
2. Linear Regression

선형 회귀란, 한 개 이상의 독립 변수 X와 종속 변수 y 간의 선형 상관 관계를 모델링하는 회귀 분석 기법이다. (출처 : 위키피디아)

Scikit-learn 라이브러리로 쉽게 많은 선형 회귀와 같은 통계적인 모델 + 기계학습 모델들을 정의하고 사용할 수 있다.

Usage

from sklearn.linear_model import LinearRegression

# 선형 회귀 모델 정의
lr = LinearRegression()

foo = lambda x: -(2/7*x**3-9/2*x**2+15*x-10.)
x_sample = np.linspace(0, 10, 5)
y_sample = foo(x_sample)

# 하나의 배치 당 하나의 feature를 가지도록 차원 추가
x_new = x_sample[:, None]

# 선형 회귀 모델에 fitting하여 학습
lr.fit(x_new, y_sample)

# Coefficient 계산
r2 = lr.score(x_new, y_sample)

# y값 예측
y_hat = lr.predict(x_new)
# 만약 하나의 데이터 포인트에 대한 예측값을 얻고 싶다면
# y_hat = lr.predict(x_new[0, None])

# Mean Squared Error 계산
MSE = np.mean((y_hat - y_sample)**2)

plt.plot(x_new, y_hat)

→ 위의 plot에 더해서 그린 경우에 대한 그래프

plot+lr

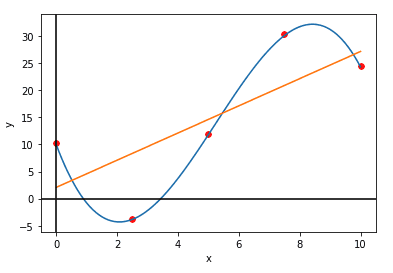
3. Polynomial Regression

다항 회귀란, 2차 이상의 다항식으로 이루어진 독립 변수 X와 종속 변수 y 간의 상관 관계를 모델링하는 회귀 분석 기법이다. (출처 : 위키피디아)

위의 선형 회귀 설명에서와 동일하게 Scikit-learn으로 구현되어 있어 쉽게 사용 가능하다.

Usage

from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures

x_sample = np.linspace(0, 10, 5)
x_new = x_sample[:, None]

foo = lambda x: -(2/7*x**3-9/2*x**2+15*x-10.)
y_sample = foo(x_sample)

# 6차 다항식으로 변환
poly = PolynomialFeatures(degree=6)
x_sample_poly = poly.fit_transform(x_new)
poly_lr = LinearRegression().fit(x_sample_poly, y_sample)

# -> x_new 출력
# Before transform: (Single features)
# [[ 0. ]
#  [ 2.5]
#  [ 5. ]
#  [ 7.5]
#  [10. ]]

# -> x_sample_poly 출력
# After transform: (Multiple features)
# [[1.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00
#   0.00000000e+00 0.00000000e+00 0.00000000e+00]
#  [1.00000000e+00 2.50000000e+00 6.25000000e+00 1.56250000e+01
#   3.90625000e+01 9.76562500e+01 2.44140625e+02]
#  [1.00000000e+00 5.00000000e+00 2.50000000e+01 1.25000000e+02
#   6.25000000e+02 3.12500000e+03 1.56250000e+04]
#  [1.00000000e+00 7.50000000e+00 5.62500000e+01 4.21875000e+02
#   3.16406250e+03 2.37304688e+04 1.77978516e+05]
#  [1.00000000e+00 1.00000000e+01 1.00000000e+02 1.00000000e+03
#   1.00000000e+04 1.00000000e+05 1.00000000e+06]]

아래의 그림과 같이, 항의 차수가 커질 수록 sample들의 특징을 더 잘 반영하여 모델링이 가능하지만 너무 커지면 Overfitting 되는 문제가 있다. 반대로, 항의 차수가 너무 낮으면 Underfitting 되는 문제가 있다.

polylr_overfitting_underfitting

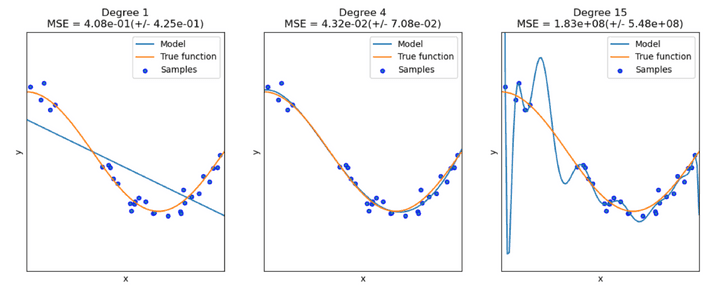
Overfitting이란, training error는 적고 variance(예측값들의 흩어진 정도)가 큰 반면, test error가 큰 현상이 나타는 문제를 말한다. 즉, training data에 대해서는 좋은 성능을 보일 수는 있어도 학습하지 않은 test data에 대해서는 좋은 성능을 보이지 못한다는 문제점을 가지고 있다.

→ Overfitting 문제에 대한 대표적인 해결책으로는 더 많은 데이터를 사용하거나 Regularization(정규화)를 하는 방법이 있다.

Underfitting은 Overfitting과는 반대로 training error와 test error가 둘 다 크며, bias(예측값과 정답값과의 차이) 또한 큰 현상이 나타는 문제를 말한다. 이는 충분히 학습되지 않아 나타는 현상이다.

→ Underfitting 문제에 대한 해결하기 위한 대표적인 방법으로는 더 많은 feature를 추가하거나 항의 차수를 증가하여 모델의 complexity를 높이거나 더 오래 학습하는 방법이 해결책이 될 수 있다.

Regularization (정규화)

Overfitting 문제를 완화하기 위한 방법 중 Regularization(정규화) 방법은 모델의 자유도를 제한하여 hypothesis space를 줄인다. 즉, 모델의 가중치들을 제한시켜 variance를 줄이고, 일반화하는 능력을 높인다. 대표적인 정규화 방식에는 1) Ridge Regression 2) Lasso Regression 3) Elastic Net 세 가지가 있다.

각 방식에 대해 하나씩 알아보자 !

Ridge Regression

Ridge Regression (릿지 회귀) 방법은 L2 Regression으로 불리며, 학습 시 Cost function (비용 함수)에 Loss의 가중치 값들에 대한 L2 regularization term을 더하여 모델의 자유도를 제한한다.

예를 들어, 6차원의 다항식 ( $w^Tx+b = w_6x^6+w_5x^5+...+w_1x^1+ b$ ) 에 대해 다항회귀를 할 때

릿지 회귀 방법에서의 비용 함수는 아래와 같이 표현된다.

L(y,y')+\frac{\alpha}{2}\lVert w\rVert^2

여기에서 $\alpha$ 는 제한의 정도(penalty) 지정하는 hyperparameter이다.

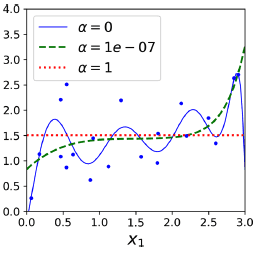
$\alpha$ 가 0이면 linear regression 이고, $\alpha$ 값이 커질 경우 모든 가중치들이 0과 가깝게 되어 예측 값이 데이터들의 평균에 가깝게 flat 한 형태가 된다.

ridge_alpha

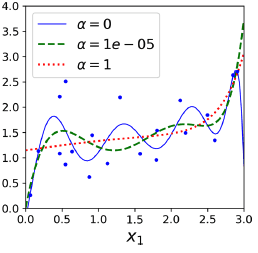
Scikit-learn 구현은 아래와 같다.

from sklearn.linear_model import Ridge
ridge_reg = Ridge(alpha=0.1)
ridge_reg.fit(X, y)
ridge_reg.predict([[1.5]])

Lasso Regression

Lasso (Least Absolute Shrinkage and Selection Operator) Regression 는 위의 Ridge regression 에서 사용한 L2 regularization 대신, L1 regularization을 하는 방법이다.

위에 설명한 6차원의 다항식을 토대로, 라쏘 회귀에서의 비용 함수는 다음과 같다.

L(y,y')+\alpha(|w_6|+|w_5|+...+|w_1|)

라쏘 회귀의 큰 특징 중 하나는 중요하지 않은 feature들의 가중치를 제거하는 경향이 있다는 것이다.

Why? 역전파(Backpropagation) 시에 비용 함수에 대해 편미분하게 되면, 가중치는 상수 값이 되어버리기 때문에, 가중치가 너무 작은 경우 0에 가까워 중요하지 않은 feature들의 가중치들의 제거하는 효과를 나타내게 된다.

위의 릿지 회귀의 그래프 이미지와 유사하면서도, 가중치를 더 작게 설정하더라도 더 flat하게 만드는 경향이 나타난다. 즉, 자동적으로 feature selection하는 효과를 나타내고 sparse model을 도출해낸다.

lasso_alpha

Scikit-learn으로 쉽게 사용 가능하다.

from sklearn.linear_model import Lasso
lasso_reg = Lasso(alpha=0.1)
lasso_reg.fit(X, y)
lasso_reg.predict([[1.5]])

Elastic Net

Elastic Net은 Ridge Regression 과 Lasso Regression의 중간으로, 두 regularization term을 섞어 사용한다. mix ratio r 으로 조절할 수 있다.

L(y,y')+r\alpha(\sum_{i=1}^n|w_i|)+\frac{l-r}{2}\alpha\lVert w\rVert^2

세 가지 정규화 방법 중에 보통 Ridge를 기본으로 많이 사용되지만, 일부 적은 feature만 유용할 때 Lasso 나 Elastic Net을 사용한다. 보통 Lasso의 경우 feature의 개수가 training instance보다 많거나 일부 feature들이 correlate될 때 예측이 어려우므로, Lasso 보다 Elastic Net이 선호된다.

Scikit-learn으로 쉽게 사용 가능하다.

from sklearn.linear_model import ElasticNet
elastic_net = ElasticNet(alpha=0.1, l1_ratio=0.5)
elastic_net.fit(X, y)
elastic_net.predict([[1.5]])

다항 회귀 vs 릿지 회귀

다항 회귀에 대해 릿지 정규화의 적용한 릿지 회귀 또한 scikit-learn 라이브러리로 쉽게 적용 가능하다.

Implementation

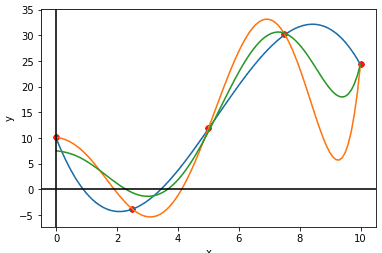
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import Ridge

x_line = np.linspace(0, 10, 100)
x_sample = np.linspace(0, 10, 5)
x_new = x_sample[:, None]

foo = lambda x: -(2/7*x**3-9/2*x**2+15*x-10.)
Y = foo(x_line)
y_sample = foo(x_sample)
# 6차 다항식으로 변환
poly = PolynomialFeatures(degree=6)
x_sample_poly = poly.fit_transform(x_new)
x_line_poly = poly.fit_transform(x_line[:, None])

# 다항 회귀 적용 및 예측
poly_lr = LinearRegression().fit(x_sample_poly, y_sample)
y_poly = poly_lr.predict(x_line_poly)

# Ridge 회귀 적용 및 예측
# penalty의 정도를 나타내는 lambda는 'alpha'라는 hyperparameter로 사용됨 !
rr = Ridge(alpha=10.0).fit(x_sample_poly, y_sample)
y_poly_rr = rr.predict(x_line_poly)

→ Plot으로 표현

(blue: 정답 값, orange: 다항 회귀 예측 값, green: 릿지 회귀 값)

plot_poly_ridge

4. Classification (Logistic Regression, Support Vector Machine, Decision Tree)

대표적인 Classification(분류) 모델으로는 다음과 같이 세 가지가 있다.

Logistic Regression (로지스틱 회귀)
Support Vector Machine (SVM) (서포트 벡터 머신)
Decision Tree (결정 트리)

Logistic Regression (로지스틱 회귀)

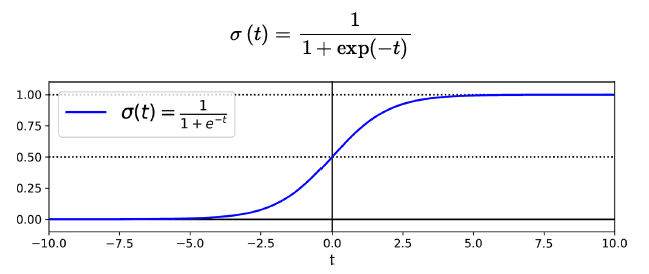
로지스틱 회귀는 선형 회귀와 같이 입력 feature들의 weighted sum을 계산하지만, 결과를 바로 출력하는 것이 아니라 결과의 logistic을 출력한다. logistic 은 sigmoid function을 뜻하며 0과 1 사이의 값을 가진다.

sigmoid

logit (log-odds) : logistic function의 역으로, positive class인지 negative class인지 측정된 확률(p)의 ratio의 log 값이다.

$logit(p) = log(p/(1-p))$

closed-form equation이 아니기 때문에, 비용함수를 최소화 하는 parameter를 계산하는 것이 어렵지만, 비용함수가 convex 형태일 경우 Gradient Descent와 같은 최적화 알고리즘을 사용한다면 global optimum을 찾을 수 있다.

multiple classes의 경우, softmax regression(multinomial logistic regression)으로 사용할 수 있다. 이 때, 클래스와 클래스 별 확률을 match하여 측정하는 cross entropy 비용 함수를 사용한다.

Support Vector Machine (SVM) (서포트 벡터 머신)

서포트 벡터 머신 분류는 쉽게 설명하자면, 분류하고자 하는 두 클래스 간의 거리(margin)를 최대화하는 모델이다. small or medium 크기의 데이터 셋에 적합한 모델이다

svm

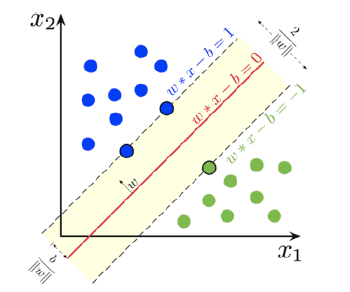
두 카테고리 중 어느 하나에 속한 데이터의 집합이 주어졌을때, 주어진 데이터 집합을 바탕으로 새로운 데이터가 어느 카테고리에 속할지 판단하는 비확률적 이진 선형 분류 모델을 만든다. 이 때, 데이터가 임베딩된 공간에서 경계(boundary)를 표현할 때 가장 큰 폭(large margin)을 가진 경계를 찾는다. 즉, 가장 가까운 각 클래스의 데이터 점들 간의 거리를 최대로 한다.

때문에, 학습이 진행되는 동안 SVM은 각 훈련 데이터 포인트가 두 클래스 사이의 결정 경계를 구분하는 데 얼마나 중요한 지를 배우게 된다. 데이터셋 전체가 아닌 클래스 사이의 경계에 위치한 데이터 포인트들이 결정 경계를 만드는 데 영향을 준다. 이러한 데이터 포인트들을 서포트 벡터(support vector)라고 한다.

선형 분류 뿐만 아니라 비선형 분류에서도 사용될 수 있으며, 선형적으로 분류가 어려운 데이터에 Feature를 더해(polynomial feature) 고차원 공간으로 대응시켜 분리를 쉽게 하는 방법을 사용한다. polynomial degree가 클 수록 모델이 느려지기 때문에, 문제에 적절한 kernel trick을 사용한다. 이는 점들의 집합과 상수 벡터의 내적 연산으로 정의하여 효율적으로 계산하도록 돕는다. 큰 데이터셋의 경우, Gaussian RBF Kernel을 사용한다.

svm_kernel

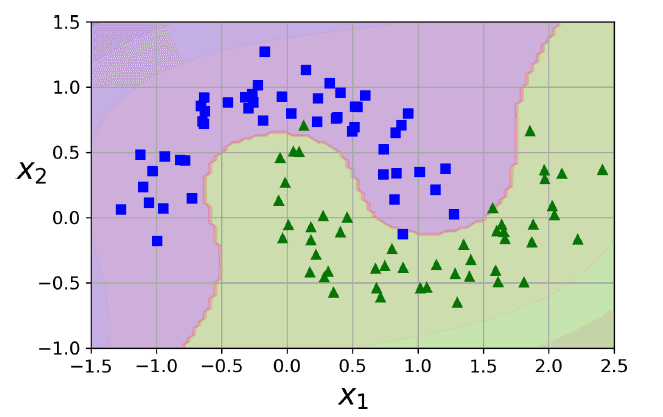
장점 : 분류, 예측에 사용 가능. overfitting 정도가 덜하다. 예측의 정확도가 높고, 사용하기 쉬움

단점 : kernel, parameter 조절 테스트를 여러번 해야 최적화된 모델을 만들 수 있음, 모델 구축 시간 오래걸림

Decision Tree (결정 트리)

결정 트리 알고리즘은 Feature에 대해 아래의 그림과 같이 트리 자료 구조 기반으로 분류한다.

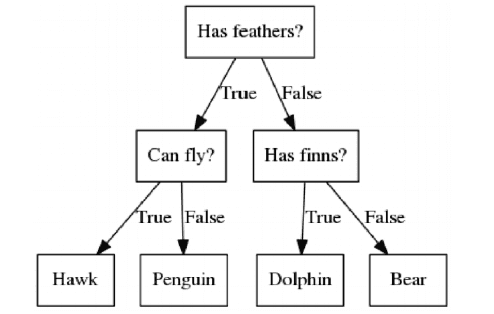
결정 트리는 feature scaling이나 centering과 같은 데이터 전처리가 필요하지 않다.

Scikit-Learn 라이브러리에서의 구현은 Classification and Regression Tree(CART) 알고리즘을 기반으로 학습한다.

먼저, 학습 데이터에 대해 하나의 feature $k$ 와 그에 대한 threshold $t_k$ 를 기준으로 두 개의 subset으로 나눈다. 이 때, threshold는 잘 분리된(Purest) Subset이 되도록 $(k, t_k)$ 쌍을 찾아서 설정한다.

J(k,t_k)=\frac{m_{left}}{m}G_{left}+\frac{m_{right}}{m}G_{right}

$G_{left/right}$ 는 left, right subset의 잘 분리되지 않음의 정도(impurity)를 뜻하고, $m_{left/right}$ 은 left, right 각 subset의 개수를 뜻한다.

Regression 문제에 적용한다면, $G_{left/right}$ 대신 $$MSE_{left/right}$ loss를 사용한다.

MSE_{node} = \sum_{i \in node}(\hat y_{node} - y^{(i)})^2 \\ \hat y_{node}= \frac{1}{m_{node}}\sum_{i \in node}y^{(i)}

max_depth parameter로 두어, 위의 과정을 재귀적으로 반복하며 depth만큼의 트리를 구축한다.

선형 모델과 달리 결정 트리 모델의 경우 학습 데이터에 대하 제한하는 정도가 적기 때문에, 학습 데이터에 트리 구조가 너무 adapt하게 학습 될 경우에 overfitting 문제가 발생할 수 있다. 파라미터가 없다기 보다 파라미터로 인한 제한이 학습 이전에 없는 모델을 nonparametric 모델이라고 부른다. 반대로 parametric 모델은 degree of freedom이 제한되기 때문에 overfitting의 위험을 줄일 수 있다. overfitting을 줄이기 위해서 freedom을 제한하기 위해 정규화(regularization)을 적용한다. 자세한 hyperparameter는 여기에 설명되어 있다.

Implementation

위의 세 모델 (Logistic Regression, Support Vector Machine, Decision Tree) 모두 Scikit-learn 라이브러리로 간단하게 구현하여 사용할 수 있다.

from sklearn.linear_model import LogisticRegression

logistic = LogisticRegression(random_state=1234)
logistic.fit(X_train[:, :2], y_train)
# softmax regression
# softmax_reg = LogisticRegression(multi_class="multinomial")

from sklearn.svm import SVC

svm = SVC(kernel='linear', random_state=1234)
svm.fit(X_train[:, :2], y_train)

from sklearn.tree import DecisionTreeClassifier
# more depth, increase decision boundary - leads to overfitting 
# similar to polynomial
dt = DecisionTreeClassifier(max_depth=2, random_state=1234) 
dt.fit(X_train[:, :2], y_train)

Reference

Aurelien Geron, Hands-on Machine Learning with Scikit-Learn, Keras, and TensorFlow, O’reilly (2019)

1. Matplotlib
2. Linear Regression
3. Polynomial Regression
- Regularization (정규화)
- 다항 회귀 vs 릿지 회귀
4. Classification (Logistic Regression, Support Vector Machine, Decision Tree)